This primer provides a gentle yet thorough introduction to elliptical key cryptography, said to be ideal for resource-constrained embedded Linux systems because it provides more “security per bit” than other types of asymmetric cryptography. The paper is from Certicom, which markets Security Builder toolkits to embedded Linux developers. Enjoy! . . .

---

An Elliptic Curve Cryptography (ECC) Primer
Why ECC is the next generation of public key cryptography
Introduction

Asymmetric cryptography is a marvellous technology. Its uses are many and varied.

And when you need it, you need it. For many situations in distributed network environments, asymmetric cryptography is a must during communications. If you're taming key distribution issues with a public key infrastructure (PKI), you're using asymmetric cryptography. If you're designing or employing any kind of network protocol or application requiring secure communications, to come up with a practical solution, you're going to have to use asymmetric cryptography.

Asymmetric cryptography has, in fact, proved so useful for securing communications that it has become pervasive in modern life. Every time you buy something on the Internet, if the vendor is using a secure server, you're using asymmetric cryptography to secure the transaction.

But asymmetric cryptography is demanding and complex, by its very nature. The hard problems in number theory — the key to the algorithms' functionality — are all intrinsically difficult enough that the processor cycles you must throw at doing it, and/or the chip space you must dedicate to the implementation, inevitably far outstrip the resources you must dedicate for doing symmetric cryptography.

That's why if you need asymmetric cryptography, you should be considering elliptic curve cryptography (ECC).

• ECC offers considerably greater security for a given key size — something we'll explain at greater length later in this paper.
• The smaller key size also makes possible much more compact implementations for a given level of security, which means faster cryptographic operations, running on smaller chips or more compact software. This means less heat production and less power consumption — all of which is of particular advantage in constrained devices, but of some advantage anywhere.
• There are extremely efficient, compact hardware implementations available for ECC exponentiation operations, offering potential reductions in implementation footprint even beyond those due to the smaller key length alone.

In short: asymmetric cryptography is demanding. But if you're looking for the cryptosystem that will give you the most security per bit, you want ECC.

This paper describes elliptic curve cryptography in greater depth — how it works, and why it offers these advantages. It will begin by discussing the larger subject of asymmetric cryptography in general.

Why Asymmetric Cryptography?

ECC is an approach — a set of algorithms for key generation, encryption and decryption — to doing asymmetric cryptography.

Asymmetric cryptographic algorithms have the property that you do not use a single key — as in symmetric cryptographic algorithms such as AES — but a key pair. One of the keys (the public key) is used for encryption, and its corresponding private key must be used for decryption. The critical feature of asymmetric cryptography, which makes it useful, is this key pair — and more specifically, a particular feature of the key pair: the fact that one of the keys cannot be obtained from the other.

Authentication With Asymmetric Cryptography

In the case of asymmetric authentication methods — the core technology behind digital signatures and certificates — we normally speak of a private key (in the possession of the entity wishing to prove its identity) and the public key (in the possession of anyone who wishes to verify the identity of the entity possessing the private key).

You may, with the public key, verify that an entity has knowledge of the private key — but you cannot derive the private key from the public. This is the critical feature of asymmetric cryptographic schemes that makes them so useful.

This property is useful for a number of things: it greatly simplifies key exchange, as one example, and it solves one critical problem symmetric cryptography cannot solve — the problem of guaranteeing unique authentication and non-repudiation. Symmetric hashing/authentication methods — ones for which there is only one key, and both parties in the exchange use it both for authentication and for signature generation — have the distinct disadvantage that they do not, on their own, offer any way to distinguish which party to the exchange signed a given message. If both or all parties must know the key, based on cryptography alone, you cannot distinguish which signed any given message, because any of them could have. In asymmetric authentication schemes, only one party knows the private key, with which the message is signed. Any number may know the public key. Since the private key cannot be derived from the public, the signature serves as a unique identifier. If the message verifies as having een signed by the
person with knowledge of the private key, we can narrow down who sent the message to one. But any number of people may have knowledge of the public key, and all of them can therefore verify the identity of the sender.

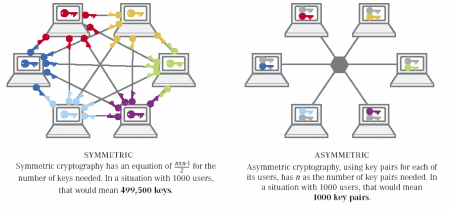
Figure 1: Symmetric vs. asymmetric keys in a meshed network
(Click to enlarge)
How Asymmetric Cryptography is Used in Digital Signatures and Certificates

Digital signatures and certificates are particularly common applications of authentication with asymmetric cryptography.

A digital signature is a transform performed on a message using the private key, whose integrity may be verified with the public key.

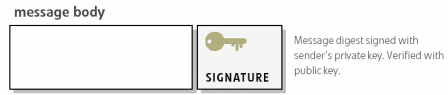
Figure 2: A digital signature
Again, the unique properties of asymmetric cryptography make it particularly useful for generating digital signatures. The correct signature may only be generated with the private key. Knowledge of the public key is only useful for verifying the signature. Any number of people may have knowledge of the public key for verification purposes, without compromising the private key. Since only one entity knows the private key, the private key serves as proof of the sending party's identity, and guarantees the integrity of messages they send.

A digital certificate is a piece of information which is digitally signed by a trusted third party, or certificate authority (CA), and which contains critical identification information, vouching for the identity of an entity. Digital certificates often themselves contain a public key corresponding to the private key the entity itself uses to prove its identity–the well-known web server certificates are examples of this type.

Figure 3: A certificate is made up of a server URL and a server public key
Encryption Using Asymmetric Cryptography

Asymmetric encryption schemes are used in a variety of applications. Probably the most visible, well-known application is in encrypted email, in peer-to-peer 'keyring' schemes such as Pretty Good Privacy (PGP).

In asymmetric encryption schemes, the public key is used for encrypting messages; these messages, once encrypted, can only be decrypted with the private key. So the recipient publishes or distributes the public key corresponding to a private key of which only they have knowledge. Anyone wishing to communicate securely with the holder of the private key encrypts his or her message using the public key. Only the recipient may decrypt and use the message; other holders of the public key cannot.

This feature of asymmetric cryptosystems greatly simplifies key exchange. In a large network of N communicating entities, if it is fully meshed, maintaining unique symmetric keys for each communicating pair of entities would require the management of (nxn-1) ÷ 2 keys. Using asymmetric cryptography, this quantity can be reduced to N key pairs. In a group of 1,000 users, it's the difference between managing 1,000 key pairs or 499,500 keys.

Functions Whose Inverse is Significantly More Difficult

In all asymmetric cryptographic schemes, this property — the property that one key is used for encryption, and another for decryption, and the decryption key cannot be found from the encryption key — is derived from the use of mathematical functions whose inverse is extremely difficult to calculate.

You may understand an asymmetric cryptographic key pair as a pair of numbers which have some relationship associated with a mathematical function which is relatively easy to compute in one direction, but whose inverse is in practical terms intractable. This feature — the function which is tractable in one direction, but intractable in the other, is common to all asymmetric cryptosystems, including ECC.

RSA — And The Integer Factorization Problem

The first asymmetric cryptosystem to have seen widespread use is also one of the most accessible illustrations of this principle in action. RSA gets its security from the difficulty of factoring very large numbers. The difficulty of getting the plaintext message back from the ciphertext and the public key is related to the difficulty of factoring a very large product of two prime numbers.

As an illustration of this: imagine you were to take two very large prime numbers — say, 200 digits long, and were then to multiply them together. Now the result you get has two particular properties:

1. It is very large (about 400 digits in length),
2. It has two, and exactly two factors, both prime numbers — the two primes you just multiplied together

You can easily — given the two prime numbers from which you start — find the product. But finding the primes given only the product is more difficult. So much more, in fact, that once the numbers get adequately large, it is almost impossible to find them. You simply cannot assemble enough computing power to do so.

So the multiplying of two large prime numbers together is the (relatively) easy forward function in this asymmetric algorithm. Its inverse — the factor finding operation — is considerably more difficult, and in practical terms, it's intractable.

The RSA system employs this fact to generate public and private key pairs. The keys are functions of the product and of the primes.

Operations performed using the cryptosystem are arranged so that the operations we wish to be tractable require performing the relatively easy forward function — multiplication.

Conversely, the operations we wish to make difficult — finding the plaintext from the ciphertext using only the public key — require performing the inverse operation — solving the factoring problem.

The Diffie Hellman/DSA Cryptosystems and the Discrete Logarithm Problem

Diffie Hellman — along with the Digital Signature Algorithm (DSA) based on it — is another of the asymmetric cryptosystems in general use.

ECC, in a sense, is an evolved form of Diffie Hellman. So to understand how ECC works, it helps to understand how Diffie Hellman works first.

Diffie Hellman uses a problem known as the discrete logarithm problem as its central, asymmetric operation. The discrete log problem concerns finding a logarithm of a number within a finite field arithmetic system.

Prime fields are fields whose sets are prime — that is, they have a prime number of members. These are of particular interest in asymmetric cryptography because, over a prime field, exponentiation turns out to be a relatively easy operation, while the inverse — computing the logarithm — is very difficult.

To generate a key pair in the discrete logarithm (DL) system, therefore, you calculate:

y=(gx)mod p

where p is a large prime — the field size. x and g are smaller than p. y is the public key. x is used as the private key. In Diffie Hellman, again, the operations we wish to make 'easy', or tractable, we harness to the operation in the field which is (relatively) easy — exponentiation. So encryption using the public key is an exponentiation operation. Decryption using the private key is as well. Decryption using the public key, however, would require performing the difficult inverse operation — solving the discrete logarithm problem.

The discrete logarithm problem, using the values in the equation above, is simply finding x given only y, g and p.

Expanding that thought slightly: someone has multiplied g by itself x times, and reduced the result into the field (performed the modulo operation) as often as necessary to keep the result smaller than p. Now, knowing y, g and p, you're trying to find out what value of x they used.

It turns out that for large enough values of p, where p is prime, this is extraordinarily difficult to do — much more difficult than just finding y from g, x and p.

If you grasp what's going on in the operations above, you're now in a position to grasp the basic math behind the DSA and discrete logarithm systems.

And, by extension, you also understand some of the principles behind ECC. ECC — as we'll discuss in greater detail a little later — also uses a discrete log problem in a finite group. The difference is that ECC defines its group differently. And it is, in fact, the difference in how the group is defined — and particularly how the mathematical operations within the group are defined — that give ECC its greater security for a given key size.

Before we discuss this, however, we should first briefly discuss why greater security at the same key size is something you might want.

For more information on Finite Fields and Diffie Hellman, read Appendix A.

Asymmetric Cryptography as a Fine Balance

As noted above, in all of the asymmetric cryptosystems, the fact that the system works at all relies upon the comparative difficulty of doing two types of operations — a 'forward' operation which must be tractable, and an 'inverse' operation which must be in practical terms intractable. In fact, in all cases, the degree of difference between the difficulties of these operations actually depends in a quite precise way on the size of the key pairs that are being generated. Both operations get more difficult as the key is made longer. The inverse operation, however, gets much more difficult, much more rapidly.

In all asymmetric cryptosystems, as mentioned above, the key length is the parameter that determines how difficult are both the forward and inverse algorithms.

As described in the preceding sections, the common characteristic of all asymmetric cryptosystems is a function whose inverse is significantly harder. We are now in a position to expand upon this: in all cases, the hardness of the forward and inverse operations is actually defined as two functions on the key length — two functions describing an 'order of growth' of the difficulty of the forward and inverse algorithms.

So, to make more precise our previous description: asymmetric cryptosystems work because the inverse operation rapidly gets more difficult as key length increases than does the forward operation.

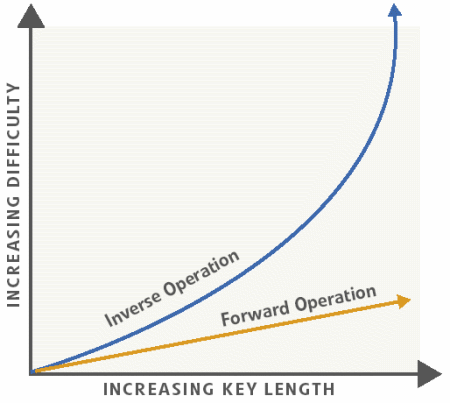
Figure 4: Difficulty of forward, inverse operation against key length
What this means in practical terms is: asymmetric cryptography is always a fine balance. Somewhere, for any given application, and any given cryptosystem, there is a key length x which is long enough that the users of the system can say the inverse operation is as hard as they need it to be to offer the level of security they desire — and yet key length x is not so long that the forward operations become unnecessarily unwieldy.

A Race Between Guns and Armour

This key length x isn't even a constant for a given cryptosystem and application. Rather, as microprocessors become faster and cheaper, a key length which seemed quite adequate a few years ago may no longer offer adequate security, as more and more processing power can be assembled to calculate the inverse function.

As a quick illustration of the speed of progress in the development of faster microprocessors, consider the following bit of history: Intel's 8086 processor, the heart of IBM's XT system, operating at a clock speed of 5 Mhz, could perform approximately .33 Millions of Instructions Per Second (MIPS).

By the year 2000, you could purchase the Pentium 4. It operated at 1.5 GHz, and could do approximately 1500 MIPS.

As a rough measure, in terms of operations per second, the processor power you can buy has increased by 1.6 every year for the past 10 years. This is commonly referred to as Moore's Law.

Moore's Law means each year chipmakers cram more gates into less and less space. Besides this, each year, clock speeds increase. And chipmakers and system builders come up with new approaches to old problems — pipelining, parallel processors, etc. Those MIPS counts keep climbing. And so key lengths in asymmetric cryptography — just as in symmetric cryptosystems — creep ever upward as a direct consequence of this progress.

Consider again the difference in the MIPS available in a cheap, readily available processor in the late 80s (.33) and in the year 2000 (1500). The processor available 20 years later can perform 4500 times as many calculations in the same amount of time.

As a rough measure, considering brute force methods of attack against a basic symmetric cryptosystem, that corresponds approximately to a key length 12 bits longer over twenty years to get equivalent security.

It's the race between guns and armour, and it's reasonable to predict it may never end. In the realm of symmetric cryptography, DES' 56 bit key is now history; it does not offer adequate security given the resources available to do brute force attacks — attacks which check every possible key. It is for this reason that the standard, which once defined DES as the appropriate symmetric encryption algorithms to use for the encryption of sensitive information within the US government, has been declared obsolete. The new standard specifies the recently developed AES algorithm, whose keys can offer 128, 192 or 256 bits of security.

ECC as the Answer for High Security and for the Future

Consider these three facets of the problem, now:

1. First, the fact that the security and practicality of a given asymmetric cryptosystems relies upon the difference in difficulty between doing a given operation and its inverse.
2. Second, the fact that the difference in difficulty between the forward and the inverse operation in a given system is a function of the key length in use, due to the fact that the difficulty of the forward and the inverse operations increase as very different functions of the key length; the inverse operations get harder faster.
3. Third, the fact that as you are forced to use longer key lengths to adjust to the greater processing power now available to attack the cryptosystem, even the 'legitimate' forward operations get harder, and require greater resources (chip space and/or processor time), though by a lesser degree than do the inverse operations.

If you understand these three things, you are now in a position to grasp the advantages ECC offers over other asymmetric cryptosystems.

ECC's advantage is this: its inverse operation gets harder, faster, against increasing key length than do the inverse operations in Diffie Hellman and RSA.

What this means is: as security requirements become more stringent, and as processing power gets cheaper and more available, ECC becomes the more practical system for use. And as security requirements become more demanding, and processors become more powerful, considerably more modest increases in key length are necessary, if you're using the ECC cryptosystem — to address the threat.

This keeps ECC implementations smaller and more efficient than other implementations. ECC can use a considerably shorter key and offer the same level of security as other asymmetric algorithms using much larger ones. Moreover, the gulf between ECC and its competitors in terms of key size required for a given level of security becomes dramatically more pronounced, at higher levels of security.

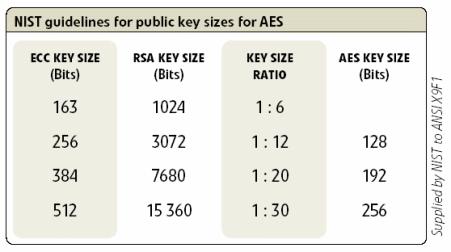
Figure 5: Equivalent key sizes for ECC and RSA
In the next section, we will describe what ECC is, and explore why its security increases more rapidly as key length increases.

What ECC Is

Elliptic Curve Cryptography, as described above, is a relative of discrete logarithm cryptography.

The DL system, as described above, relies upon the difficulty of the discrete logarithm problem — a logarithm problem calculated within the multiplicative group of a finite field — to frustrate attempts to use the public key to compromise the private one.

ECC uses groups and a logarithm problem too.

What ECC also offers, however, is a difference in the method by which the group is defined — how the elements of the group are defined, and how the fundamental operations on them are defined.

It's the difference in the way the group is defined–both the numbers in the set and the definitions of the arithmetic operations used to manipulate them–that give ECC its more rapid increase in security as key length increases.

To clarify this point, we'll describe briefly how elliptic curves are defined.

Elliptic Curves

The way that the elliptic curve operations are defined is what gives ECC its higher security at smaller key sizes.

An elliptic curve is defined in a standard, two dimensional x,y Cartesian coordinate system by an equation of the form:

y² = x³ + ax + b

The graphs turns out to be gently looping lines of various forms.

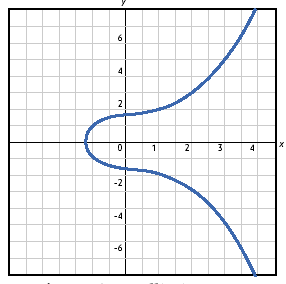
Figure 6: an elliptic curve
In elliptic curve cryptosystems, the elliptic curve is used to define the members of the set over which the group is calculated, as well as the operations between them which define how math works in the group.

It's done as follows: imagine a graph labeled along both axes with the numbers of a large prime field. That is to say: a square graph, p x p in size, where p is a very large prime number. Fp is the field of integers modulo p, and consists of all the integers from 0 to p-1.

Now the prime numbers actually employed in practical ECC implementations are quite large, so it's difficult to visualize this graph if you use the real kinds of numbers used. But as an exercise, you can imagine a more comprehensible prime — such as 17. So you'd be looking at a graph 17×17 units in size.

Now if you define an elliptic curve — an equation of the form given above — so that there are points (x, y) on the curve that satisfy the condition that both x and y are members of the prime field, you have implicitly created a group from the set of integer points on the curve; it is a subset of all the points in the p by p matrix created when you drew the graph — specifically the ones the curve passes directly through.

Note that unlike the groups used in Diffie Hellman, the elements of the set aren't integers, but points. But the system that will result is still going to be, in most senses, the same, familiar arithmetic system as those discussed above. It contains a set of elements (points, in this case), and when you add one point to another, or subtract one from another, there are rules that say what point in the set you wind up at when you do so — just as for the integers in the groups used in Diffie Hellman. And these rules still follow many of the familiar rules for the arithmetic you already know.

Industry use
* Elliptic curve groups over the finite fields of GF(p) and GF(2m)
* Koblitz EC groups over GF(2m) can be faster than GF(p)

NIST recommended curves:
* Over GF(p): P-192, P-224, P-256, P-384, P-521
* Koblitz GF(2m): K-163, K-233, K-283, K-409, K-571
* Non-Koblitz GF(2m): B-163, B-233, B-283, B-409, B-571

For more information on Elliptic Curve Group Operations see Appendix B.

Point Multiplication

The dominant operation in ECC cryptographic schemes is point multiplication. This is the operation which is the key to the use of elliptic curves for asymmetric cryptography — the critical operation which is itself fairly simple, but whose inverse (the elliptic curve discrete logarithm problem — defined below) is very difficult. ECC arranges itself so that when you wish to perform an operation the cryptosystem should make easy — encrypting a message with the public key, decrypting it with the private key — the operation you are performing is point multiplication.

Point multiplication is simply calculating kP, where k is an integer and P is a point on the elliptic curve defined in the prime field.

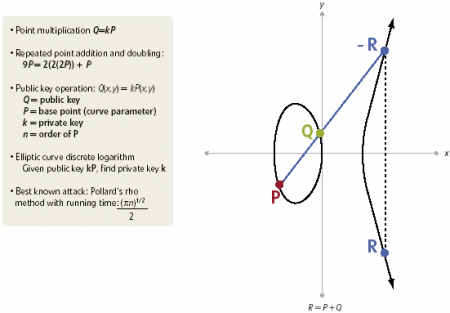
Figure 7: Eliptical curve cryptography
(Click to enlarge)
In terms of the addition operation we defined above, and the corresponding diagram, you can see how the following would look: take a point, add it to itself (doubling). Then take the result, and the original point, and add them together again, using the chord and tangent rule. Then take that result, and the original point again, and use the chord and tangent rule yet again. And so on — doing one doubling, and k-2 chord and tangent additions, until you've added P to itself k-1 times, giving kP.

Now if the only way of doing this were in fact to repeat those precise operations — finding the points P, 2P, 3P, and so on up to kP — elliptic curves would be useless for cryptography, since the operation which searches for k given only P and kP (see the elliptic curve discrete logarithm problem, below) would be no harder than doing this. You could thus search for k from kP as quickly as you could calculate kP directly given p and k.

However, there are shortcuts for point multiplication. Given the known shape of the curve, there are in fact several algorithms available which run in considerably less time than would such a stepwise operation. Which of them you choose to use depends on a number of factors — including which calculations you might be able to do ahead of time (which is practical for some cryptographic protocol purposes, in which P is known ahead of time), how much RAM you can set aside for lookup tables, and that sort of thing.

None of the operations is exactly what you'd call trivial. But all of them are vastly easier than doing it by stepwise addition — easier by many orders of magnitude. And they also run in nearconstant time for a given field size, regardless of what k and P you feed them as input. Some of the fastest working are in the NIST P192 curve, defined using the prime 2¹⁹²-2⁶⁴+1. Here, you are able to get kP in the equivalent of 38 addition and 192 doubling operations, when counting only those which are usable even when P isn't known ahead of time.

You can do better still, in fact, in hardware implementations, in fields of order 2^m. In these fields– the fields called binary fields, or characteristic two finite fields–hardware implementations that take advantages of opportunities for parallel processing, multiplication has been accelerated.

Now these still aren't trivial operations. But the important thing is this: compared to what the attacker has to do to get k back from kP, it's nothing. Which brings us to the inverse operation.

The Elliptic Curve Discrete Logarithm Problem

The inverse operation to point multiplication — finding a log in a group defined on an elliptic curve over a prime field — is defined as follows: given points Q and P, find the integer k such that Q=kP.

This is the elliptic curve discrete logarithm problem — and this is the inverse operation in the cryptosystem — the one you effectively have to perform to get the plaintext back from the ciphertext, given only the public key.

Now naively the obvious, certain way of finding k would be to perform repeated addition — operations — stepping through P, 2P, 3P, and so on, until you find kP. You'd start by doubling P, then adding P to 2P finding 3P, then 3P to P finding 4P and so on. This is the brute force method. The trouble with this is if you use a large enough prime field, the number of possible values for k becomes inconveniently large. So inconveniently large that it's quite practical to create a sufficiently large prime field that searching through the possible values of k would take all the processor time currently available on the planet thousands of years.

In the case of the NIST-defined P192 curve used as an example above, you'd have to do (on average) a doubling followed by on the order of 3×10⁵⁷ additions. In the worst case, you'd have to do twice as many additions.

It is probably unnecessary at this point to point out that 3×10⁵⁷ is really a very, very large number. And a lot larger than the few hundreds of operations we needed to do the multiplication in the first place.

This may sound unfair. And it is. It's so grossly unfair, in fact, that you can, conveniently, do those multiplication operations in the rather limited processor of a tiny little handheld Blackberry unit or cellular phone operating on a 2.5 V battery in the course of routine communications, in a handshake at the beginning of a secure exchange, in considerably less than a second. And you can then quite safely send kP through the air where anyone can hear it. Indeed, you can publish kP and ask other people to use it as a component of the public key via which they communicate with you. And then that someone can take kP and go looking for k — the value you've kept to yourself for use as your private key. And even if that someone isn't restricted to a portable phone and less than a second — even if that someone has a cave full of the latest massively parallel supercomputers and several years — even then, they're still not getting k back.

That's basically because 3×10⁵⁷ divided by a few hundred adds up to an awfully large number. Though there is a bit more to the story we have to get to now, to distinguish between how difficult it is to break ECC versus how difficult it is to break Diffie Hellman and RSA.

Pollard's rho Attack Versus Index Calculus

As we noted earlier in this paper, there is a profound difference in the difficulty of the forward and inverse operations at the centre of all popular asymmetric schemes — that is the soul of their usefulness. In RSA, it's integer multiplication (forward) and factorization (inverse) that make the system work. In Diffie Hellman it's discrete exponentiation (forward) and log (inverse). In ECC it's point multiplication (forward) and the elliptic curve discrete logarithm problem (inverse).

In all of these cases, it's easy to see that the difficulty of the brute force approach to the inverse operation increases exponentially with the size of the key. Simply look at the number of values that must be tried; it doubles with each bit added to the key length.

Now it turns out that for all of these cryptosystems, the brute force method isn't quite the best you can do. You can, in fact, for Diffie Hellman and for RSA, try to retrieve the private key from the public (or the plaintext from the public key and the ciphertext) via the index calculus method. It's difficulty grows subexpotentially with the key length.

There are, in other words, shortcuts for doing the inverse operations, just as there was a shortcut for doing point multiplication.

The difference is, the shortcuts for doing the inverse operations aren't good shortcuts. A typical number field sieve variant of the index calculus method — the best you can do for Diffie Hellman — gets subexponentially more difficult as the field size increases –technically at a rate of e^{1.9(lnn)1/3(lnlnn)2/3} where n is the field size which is itself, remember, exponential to the key length. It's not as steep an increase as 2^k, where k is the key length — but a graph of the number of steps you must perform (on average) to find a key via the index calculus method versus the key size is still pretty steep.

And that's the point. That curve of number of steps versus key size — and the index calculus attack it describes — are what you have to keep in mind when you choose your key length in doing asymmetric cryptography. And that's the calculation you're actually doing when you choose the size of your RSA and your Diffie Hellman keys. How big do I have to make this so the best attack available — index calculus, in this case — is still too much trouble, for now and for some decades, assuming hardware continues to get faster at roughly the rate it has in the past? And that's the estimate you're counting on when you chose that 2048 bit key, and assume it's good enough for the useful life of your product–a figure taken as being 20 years and up, usually.

And that's where ECC really starts to shine.

Index calculus attacks are demanding enough that asymmetric cryptography is feasible despite them, provided the key is kept large enough.

But ECC can do better, and with smaller keys.

And that's because ECC cryptosystems aren't vulnerable to index calculus attacks. Index calculus attacks rely on certain group properties not present in groups defined using elliptic curves

The best you can do for ECC is another attack — a more general-purpose attack called Pollard's rho attack.

Pollard's rho attack is a class of what are known as 'collision search' attacks. They also do better than brute force. But they also get a lot harder a lot faster than do the index calculus attacks, as the field size increases.

Pollard's rho attack gets more difficult as ÷(πn)/2, where n is the group size (again, remember, itself exponential to the key size). The resulting curve — a plot of the number of operations against key length — is considerably steeper than is the curve for the index calculus attack described above.

—
1 Astute readers will note that the prime p, using P192, is around 6.2×10⁵⁷. And though there are actually therefore (6.2×10⁵⁷)² points in the graph you draw, it turns out the curve usually intersects around p points, giving a final field size not far from the size of the prime itself.

2 Note–there are subexponential running time attacks against certain, specific ECC groups, defined on certain curves; but these curves are easily avoided.
—

Conclusion

ECC for Portable Devices, Applications …and for the Future

And this, in the end, is the reason ECC is a stronger option than the RSA and discrete logarithm systems for the future. And this, in the end, is why ECC is such an excellent choice for doing asymmetric cryptography in portable, necessarily constrained devices right now.

As an example: as of this writing, a popular, recommended RSA key size for most applications is 2,048 bits. For equivalent security using ECC, you need a key of only 224 bits.

The difference becomes more and more pronounced as security levels increase (and, as a corollary, as hardware gets faster, and the recommended key sizes must be increased). A 384 -bit ECC key matches a 7680-bit RSA key for security.

The smaller ECC keys mean the cryptographic operations that must be performed by the communicating devices can be squeezed into considerably smaller hardware, that software applications may complete cryptographic operations with fewer processor cycles, and operations can be performed that much faster, while still guaranteeing equivalent security.

This means, in turn, less heat, less power consumption, less real estate consumed on the printed circuit board, and software applications that run more rapidly and make lower memory demands. Leading in turn to more portable devices which run longer, and produce less heat.

In short, if you're trying to make your devices smaller–and if you need to do asymmetric cryptography, you need ECC. If you're trying to make them run longer on the same battery, and produce less heat, and you need asymmetric cryptography, you need ECC. And if you want an asymmetric cryptosystem that scales for the future, you want ECC. And if you just want the most elegant, most efficient asymmetric cryptosystem going, you want ECC. If you just want the most elegant, most efficient asymmetric cryptosystem going, you want ECC.

Appendix A: Finite Fields and Diffie Hellman

A finite field is a finite set of numbers and a set of rules for doing arithmetic with the numbers in that set.

Usually, you define two operations in defining a field — one rule for adding two of the set members together to arrive at a third set member — and another operation which gives the rule for multiplication. Subtraction and division are defined in terms of addition and multiplication, respectively, and all other operations are defined in terms of these four. Essentially, therefore, you can view a finite field as a sort of self-contained, fully defined system of arithmetic. In many ways, the systems are very much like the normal system of arithmetic you're used to working with — the one you learned in grade school.

There are however, some differences in the case of the finite fields used in cryptography. The two big differences are:

1. The number systems contain only integers, and
2. The number systems are finite in size

The principal similarities are that you can add, subtract, divide, and multiply within them. All the basic operations are defined, and they work much the same as they do in normal arithmetic.

There is one odd feature, however, about the math, which follows from the fact that the field is finite in size: the field, in essence, 'wraps around'. Since all operations on the set must have a result that maps back into the set, if you add two numbers and get a result that would take you outside the set, you reduce the number so it maps back into the set. The operation used to do this in many finite fields is modulo: you divide the number by the size of the set, and take the remainder–as a trivial example, in a finite field of 7 elements, 2+13=1. This is because 2+13 = 15, and 15 mod 7 is 1.

The members–excluding 0–of a finite field, together with the multiplication operation, form a group. This group is called the multiplicative group of a finite field.

Appendix B: Elliptic Curve Group Operations

The group operations — the manipulations you perform to add one member to another, and subtract one from another — are defined based on the curve.

They work as follows:

To add point a to point b, you draw a line between the two points. That line always intersects the curve at a third point — point c.

You then draw a vertical line through point c. That line will intersect the curve at a fourth point — point d — the reflection of c in the x-axis.

Point d is taken as the result of summing points a and b.

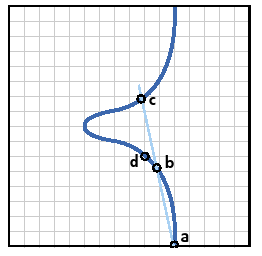
Figure B1: addition a + b = d
The double of point a is found as follows: draw a tangent line to the curve at a. The line will intersect the curve at a second point, b. Draw a vertical line through b. This intersects the curve at c, the reflection of b about the x-axis. c is the double of a.

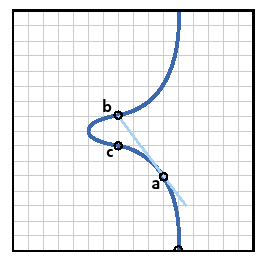
Figure B1: Doubling rule: 2a = c
From these basic operations are derived all the remaining mathematical operations that can be performed in the field. Including the critical one for cryptographic purposes — point multiplication — and its very intractable inverse — discrete log.

This whitepaper is copyright Certicom, and is reproduced by LinuxDevices.com with permission. Additional Certicom whitepapers are available online.

 
This article was originally published on LinuxDevices.com and has been donated to the open source community by QuinStreet Inc. Please visit LinuxToday.com for up-to-date news and articles about Linux and open source.